[译]背景:着色的物理和数学(2)
(译者注:本文是翻译的Naty Hoffman的《Background: Physics and Math of Shading》。我希望通过翻译此文,彻底理解PBR的原理。某些我实在不知道如何恰当翻译的地方,就把英文原文也放上了。)
表面反射(Specular项)
基于物理的BRDF的specular项通常都是基于微平面理论(microfacet theory)的。这一理论用于描述一般(非光学平滑的)表面的反射光。微平面理论的基础假设是,表面变化(微观几何形态)发生的数量级小于观察粒度(着色像素解析度)且大于可见光波长(因此几何光学有效而衍射等现象可以忽略)。到目前为止,微平面理论只能被用于继承single-bounce表面反射的说法;对于multiple-bounce表面反射的综合理论还是个未解的难题。
既然微观几何形态被假设为远大于可见光波长,那么表面上每个点处都被视为光学平滑的。如前文所述,光学平滑的表面将光拆分为两个方向:反射方向和折射方向。
表面上的每个点处,都将入射光反射到一个单独的出射方向上,出射方向依赖于微观几何形态的法线m。当求去BRDF的值时,需要输入入射光方向l和观察者方向v。这意味着,只有那些恰好法线位于m的点上才对BRDF有贡献。在Figure 22中,我们可以看到这些“正确排布”的表面点处的法线m恰好是l和v的中间。这个在l和v之间的向量被称为半向量或半角向量,我们用h表示它。
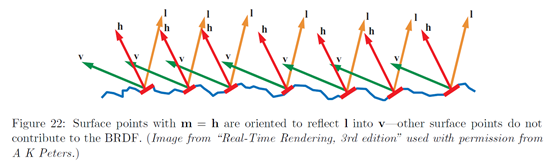

并非所有的m=h处的点都对反射有贡献;有的被其他区域的入射光方向格挡(形成阴影),有的被从出射方向格挡(形成屏蔽),有的两者都有。微平面理论假设所有被格挡了的光都从specular项中损失掉了;现实中,由于多次表面反射,某些被格挡了的光最终会反射出来,但在微平面理论中不计入这个情形。光-表面交互的多种情形如Figure 23所示。
有了这些假设(局部光学平滑,没有相互反射),BRDF的specular项可以由参考资料[1, 73]的原则推理出来。它有如下的形式:
 (4)
(4)
我们会详细讲解这里的每个小项,但首先来总评一下。D(h)是微观几何形态在半角向量h上的一个法线分布函数;换句话说,就是能够反射l到v的表面点的比例。G(l, v, h)是几何函数;它告诉我们,所有m=h的点中,没有被格挡的比例。因此,D和G函数的乘机就给出了有效表面点的比例,即真正参与了反射l到v的那些点的比例。F(l, h)函数是有效表面点的菲涅耳反射率。它告诉我们每个入射光l有多大比例被反射。最后,分母4(nl)(nv)是个矫正因子,负责将量从围观几何形态的局部空间转换到全局的微表面。(译者注:我也不懂这句是什么意思)
菲涅耳反射率
菲涅耳反射率方程计算光学平滑的表面反射光的比例(译者注:1-此值就是折射光的比例)。它的值依赖于两件事:入射角和材质的折射率。由于折射率在可见光光谱上是变化的,菲涅耳反射率显然是个光谱量——便于生产实际起见,是个RGB三元组。我们也知道每个RGB值都在[0, 1]范围内,因为一个表面不能反射低于0%或者高于100%的的入射光嘛。
完整版的菲涅耳方程还是比较复杂的。退一步说(即使不复杂),所需要的材质参数(在可见光光谱上密集采样得到复数折射率)对艺术家也不方便用。但是,通过观察现实世界中材质的表现,我们可以找到一个参数更方便使用的简化版本。按此思路,我们来看一下Figure 24所示的图。
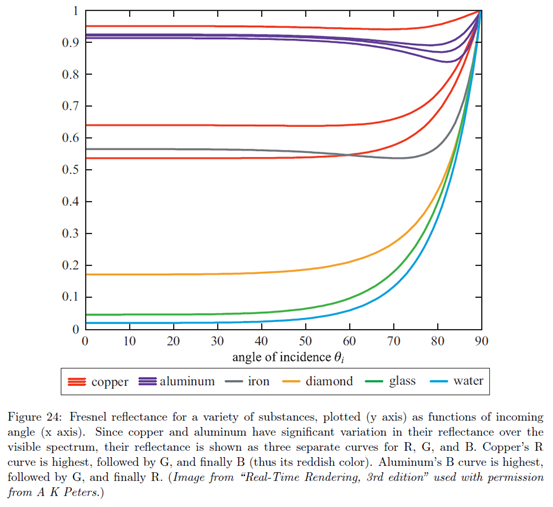
此图选取的材质范围广泛。尽管如此,也可以看到一些它们的共同之处。在入射角为0°-45°范围内,辐射率几乎是不变的。辐射率在45°-75°之间变化得比较明显(一般是增加,但不是所有材质都增加)。最后,辐射率在75°-90°之间都迅速增长到1(对应了白色)。
通过一个简单的三维场景来观察这些数值和角度的变化是有益的。暂且把微平面理论放到一边。我们看一个更简单的情形:光学平滑的金属表面的反射。这样的表面会将每个入射光反射到唯一的一个出射方向。用BRDF描述这个行为不方便(它坍缩为一个delta函数),但是有一个简单得多的方法来建模渲染它:从观察者方向采集入射光辐射率,然后用它乘以菲涅耳反射率,这就是出射光辐射率。这个方法对于能从任何方向表述入射光的光照模型都好用(光照模型将在本文后续章节介绍)。本例中,菲涅耳反射率的“入射角度”应当是表面法线n与观察者向量v之间的角度(入射方向应是v围绕n的反射向量)。Figure 25展示了这个角度(以及导致的菲涅耳反射率)在一个简单的三维场景中是如何变化的。我们可以看到绿色和黄色区域占主导地位——菲涅耳反射率在大部分可见像素上都没有改变,只在边缘上才有显著的增加。

在微平面理论中,我们处理的不是光滑表面,而是局部光滑的微观几何体。本例中,我们关心的是各个表面点上的菲涅耳反射率。由于对BRDF有贡献的所有表面点的围观几何体的法线都是半角向量h(回忆Figure 22),显然h就应当是被用于计算菲涅耳反射率的向量。那么菲涅耳入射角度就是h和l之间的角度(用v代替l也可以,反正最后结果都是相同的)。
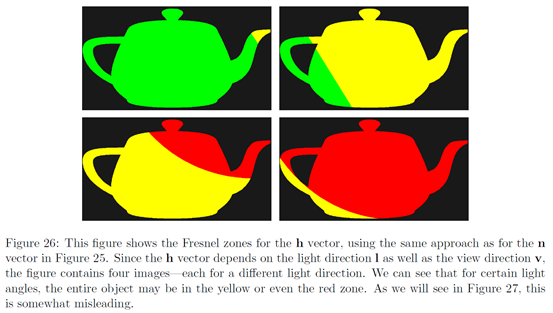
Figure 26可视化展示了h和l之间的角度,方法与Figure 25可视化n和v之间的角度相同。从此图可以看到,在某些角度的光照下,黄色甚至红色区域都可能占主导地位。然而,如我们在Figure 27中所见,这是个误会;当BRDF的其他部分被计算进来后,很清楚可以看到红色区域(反射率急速增长的地方)只局限于边缘上。

既然菲涅耳反射率在给定的三维场景中的大部分可见位置都保持着0°时的数值,我们可以把这个数值(我们将用F0表示)看作材质的specular反射率特征。这个值有颜色的属性——它就是一个RGB值,介于0和1之间。它是光的选择性反射率的度量。(译者注:我也看不懂)因此,我们也将此值称为表面的specular颜色。
F0看起来是菲涅耳反射率的理想近似,实际上Schlick[63]给出了一个简易又足够精确的用法:
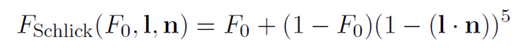 (5)
(5)
这一近似公式广泛用于计算机图形学(游戏中有时使用一个基于球形高斯函数的稍微更简易的近似)。在用于微平面BRDF时,表面法线n必须被有效的微观几何体的法线h替代:
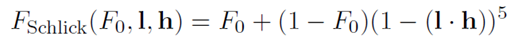 (6)
(6)
为了找到F0的恰当的值,观察一下现实世界的材质的F0是有用的。这可以在Table 1找到。它给出了线性空间和gamma(sRGB)空间的值;我们建议任何不了解在线性空间着色(以及将gamma空间的数据转换到线性空间等问题)的重要性的人,参考一下相关话题的文章[30, 34, 69]。
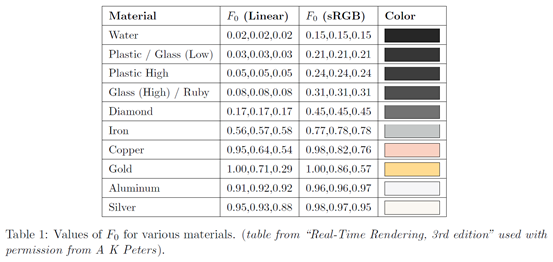
查看Table 1的时候,会发现几件事。一是金属的F0明显高于非金属。即使是铁这种相对暗淡的金属,在0°的时候都能反射超过50%的入射光。回忆一下,金属没有下表面反射,明亮的specular颜色,没有diffuse颜色,这是金属的明显的视觉特征。另一方面,钻石,这种最明亮的非金属,在0°的时候只反射17%的入射光。大多数非金属反射的量明显小于它。极少数材质的值位于20%到40%的“无人区”,这些一般是半导体或异域风情的材质,它们不太可能出现在着色产业环境中。低于2%的材质(水的F0)也是这样。实际上,除了金属,宝石,水晶,你在实验室外能看到的基本上所有材质的F0都在2%到5%这一窄窄的范围内。
法线分布函数
大多数表面上的微观几何体的表面点的朝向没有统一的分布。表面点中法线“向上”(朝向微观法线向量n)的比“朝一边”的多。表面朝向的统计学分布由微观几何体法线分布函数(microgeometry normal distribution function)D(m)定义。与F()不同,D()的值不限于[0, 1]——虽然必须是非负数,其值可以是任意大(表示法线朝向某个方向的表面点非常多)的。而且,D()也不是光谱学的,不是颜色,它是个标量。在微平面BRDF项,D()是为了与方向h比较,以帮助找到潜在的有效表面点(m=h的那些)的数量。这就是为什么法线分布函数D(h) 会出现在Equation 4中。
函数D(h) 决定了specular高光的尺寸、亮度和形状。图形学文献中提供了几种不同的法线分布函数。很多都是高斯系列再加上某种“粗糙度”或者变量做参数,然而各向异性函数一般都有2个粗糙度参数(最近发表的一些文献中的各向同性函数也有2个参数(as do some recently published isotropic ones)[4, 10, 51])。随着表面粗糙度降低,微观几何体的法线m围绕表面整体法线n的集中度就增长,D(m) 函数的值就可能变得很大(在m=n的极限处,其值是无限大的)。Walter et al. [73]讨论了分布函数的标准化问题,并给了几个例子;在其他文献[2, 3, 4, 10, 44, 51, 74]中有更多的例子。Reed [62]给出了法线分布函数的另一种解释(译者注:D(m) 的另一种理解方式)。
几何函数
几何函数G(l, v, h)表示,对于一个给定了微观几何体法线m的表面点,它能同时被 光线方向l和观察者方向v看到的概率。在微平面BRDF中,m被h代替(理由同上)。既然G()函数表示一个概率,它的值就是个标量,范围为[0, 1]。在文献[2, 3, 15, 16, 41, 44, 73]中有多种G()函数的解析表达式,它们通常是基于表面的简化模型而得的近似解决方案。G()函数没有给BRDF引入新的参数,它要么不使用参数,要么使用D()函数中的粗糙度参数。很多情形下,G()函数抵消了Equation 4中的一部分分母(nl)(nv),用其他表达式代替了它。
G()函数对于BRDF保持能量守恒是必须的——没有这一项,BRDF可能反射出比它收到的多得多的光能。微平面的BRDF推导的一个关键部分,就和(有效表面面积(从l到v反射光的表面区域))与(全部表面面积)的比例有关。如果不计入阴影和遮蔽,那么有效面积会超过全部面积。这种能量不守恒(有时非常不守恒)明显不可能出现在客观世界(见Figure 28)。

微平面模型的局限
微平面理论的公式相当强大和灵活,它允许通过(改变参数值(specular颜色、法线分布的粗糙度)或某些子项的形式(法线分布函数、几何函数))给出多种不同的渲染效果。但是,有几种现象是它不能建模的(译者注:不能拿它套用的)。如果要渲染这些现象,那么对它们进行修改或扩展就是必须的。
微平面模型没有考虑波动光学效应,例如衍射和干涉。这不是大问题,因为这种效果在渲染产业中不常出现。等真出现的时候,特别是技术会用来处理它们,而不是基于物理的建模技术。(译者注:“毒蛇出没之处,七步之内必有解药”——《神雕侠侣》)(“光滑表面”特性在接近可见光波长的尺寸时)或者(更大的表面特性由于在掠射角[76]的投影缩减效应下变得更小时)会导致更多的微妙的波动光学效果。已发表的针对这些效果的模型变都是彻底的波动光学模型[33, 68],由于其太过复杂,还没有见到太多产业成果。针对这些效果的更加产业友好型的模型开发会很受期待。光学工程领域里一些有希望的模型已经开始影响到图形学文献[51]了。
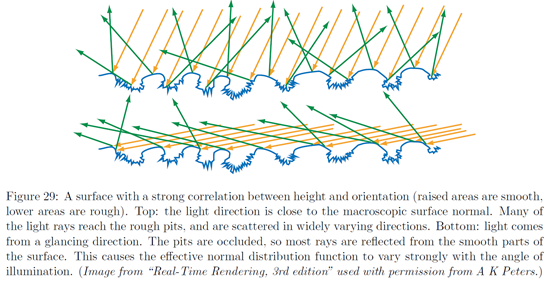
另外,微平面模型是基于相对受限的表面微观几何体模型和几个不明确的假设(译者注:应该是有时候靠不住的假设)。例如,法线分布函数的定义,它假设可见的微观几何体表面的朝向不随观察者方向的变化而变化。这等于假设微观几何体的高度和法线是不相关的[1]。但是,这个假设并非永远为真,这就会影响BRDF。想象一个表面,开始时,其粗糙度各处相同,然后,隆起的部分被摩擦地很光亮。从掠射角看,只有隆起的部分是可见的,这使得表面明显比在其他角度看起来更光滑。见Figure 29。
最近有研究表明,在某些情况下,对基础微平面模型的其他构造方式或修改可能产生更适合测试数据的结果——大多数是上文讨论的情况的组合。这些结果尚需更多的研究探索。
作为表面反射的理论基础,微平面理论尽管最终可能会被代替(或者至少被扩展),目前它还是我们手上最被理解的和最成功的工具。因此,本文后续部分将专注于微平面模型。
(译者注:“模型”这个词有多种理解。在“微平面模型”里,它的含义和“经济学模型”最接近。在“三维模型”里,它是另一个意思,是指*.obj,*.3ds,*.max这样的文件。)
下表面反射(Diffuse项)
未完待续。。